Three years in, I am still absolutely hooked on the Traitors (the TV series). Sure, yes, they stretch ten minutes of gameplay into sixty minutes of “you know I love you, but…” and the weirdly maddening attempts to make “yourself” a polite version of “you”. And yes, there’s massive thumb-shaped groove on the scales because the producers are never going to let the game end early. But all the same, it’s such fun watching the players plot and scheme and make terrible, terrible decisions.

Occasionally the show includes contestants who are expert game players. Frankly they tend to underwhelm - with the honourable exception being Kate in Traitors Australia - yet it makes me wonder about optimum strategies. And what’s more fun than playing a game? Making a model of the game in R!

Here we go, starting with a simple model and building up to more realistic strategies. If you’re here just for some insights into the Traitors, you can skip over the code without missing much of the logic.

Code

#  Plumbing and other irrelevant code is behind the folds.
library(knitr)
library(tidyverse)

set.seed(42) # trad

orange <- rgb(236 / 255, 137 / 255, 51 / 255)
mauve <- rgb(89 / 255, 14 / 255, 50 / 255)

Simple model

The minimum players for Werewolf, a.k.a. Mafia (the game on which Traitors is based) is six, with four villagers and two wolves. In this version of the game there is no recruitment and there are no shields. Let’s model this simple version and build up from there. We’ll set some basic default strategies for the traitors and the faithful.

game <- function(
    n_players = 6,
    n_traitors = 2,
    traitor_strategy = random_traitors,
    faithful_strategy = random_faithful) {

  while (TRUE) {

    # There's an implicit player index:
    #  c(traitor, traitor, faithful, faithful, ..., faithful)

    # Traitors are always the leading elements in the index, so we can select them with an index range.

    # End-game condition
    if (n_traitors == 0 || n_players - n_traitors < n_traitors) {
      break
    }

    #############
    # DAY PHASE #
    #############

    # Traitors and faithfuls update the votes array according to their strategies
    
    votes <- rep(0, n_players)

    if (n_players - n_traitors == 1) {
      # special case for 2 players 1 traitor
      # coded here to avoid having to handle it repeatedly
      votes[1:n_traitors] <- n_players
    } else {
      votes[1:n_traitors] <- traitor_strategy(n_players, n_traitors)
    }
    votes[(n_traitors + 1):n_players] <- faithful_strategy(n_players, n_traitors)

    # Claudia counts the votes
    banished <- which.max(tabulate(votes))

    n_players <- n_players - 1 # BANISHMENT!

    # If it was a traitor who was banished, decrement
    if (banished <= n_traitors) {
      n_traitors <- n_traitors - 1
    }

    # Check if the game is done yet
    if (n_traitors == 0 || n_players - n_traitors < n_traitors) {
      break
    }

    ###############
    # NIGHT PHASE #
    ###############
    n_players <- n_players - 1 # MURDER!
  }

  list(n_players_remaining = n_players, n_traitors_remaining = n_traitors)
}

random_faithful <- function(n_players, n_traitors) {
  # vote for a single random player
  target <- sample(1:n_players, size = 1)
  rep(target, n_players - n_traitors)
}

random_traitors <- function(n_players, n_traitors) {
  # vote a single random faithful
  target <- sample((n_traitors + 1):n_players, size = 1)
  rep(target, n_traitors)
}

# Simulate one random game
game()

$n_players_remaining
[1] 1

$n_traitors_remaining
[1] 1

That’s it. All we need to do now is simulate a lot of games and analyse the results. dplyr is our friend for this, as usual.

sim_games <- function(..., .game = game, .n_games = 10000) {
  1:.n_games |>
    map(\(x) .game(...), .progress = TRUE) |>
    bind_rows() |>
    mutate(
      traitors_win = n_traitors_remaining > 0,
      winner = ifelse(n_traitors_remaining > 0, "Traitors", "Faithful")
    )
}

plot_game_results <- function(results, n_players, n_traitors) {
  traitor_win_prob <- mean(results$traitors_win)

  ggplot(
    results |>
      group_by(winner) |>
      count()
  ) +
    aes(y = winner, x = n, fill = winner, label = winner) +
    geom_bar(stat = "identity", colour = "black", orientation = "y", alpha = 0.9) +
    scale_fill_manual(values = c(mauve, orange)) +
    labs(
      title = sprintf(
        "Game result for %s players, %s traitors. Traitor win prob: %s",
        n_players,
        n_traitors,
        round(traitor_win_prob, digits = 2)
      ),
      x = "Wins",
      y = NULL,
      fill = "Winner"
    ) +
    theme_minimal() +
    theme(aspect.ratio = 0.5)
}

results <- sim_games(6, 2)
plot_game_results(results, 6, 2)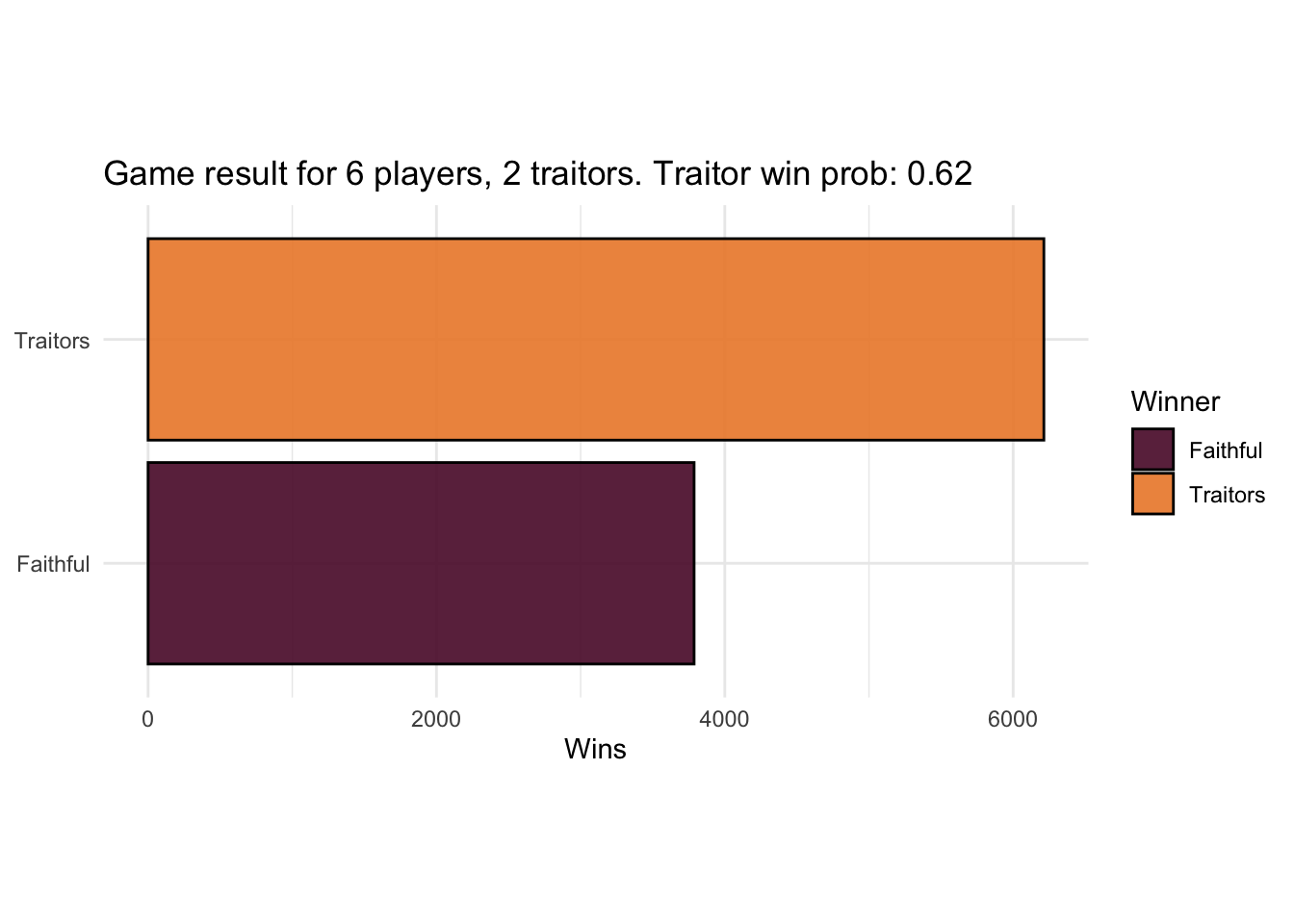

That’s quite in favour of the traitors, but the picture is different when we change the balance to be the same as the show.

results <- sim_games(22, 3)
plot_game_results(results, 22, 3)

Now the game is nearly perfectly balanced.

To check this simulation is on the right track, I had a little look at a paper on Mafia by Migdał, 2024, which includes this formula for traitor winning probability:

\[ p(n, m) \propto \frac{m}{\sqrt{n}} \]

Where \(n\) is the number of players, \(m\) is the number of traitors, and \(p\) is the winning probability.

Migdał calculates the exact probabilities for games with a single traitor and a pseudo-random faithful vote strategy, so we can compare the simulation to the calculation.

The formula in this case is:

\[ p(n, 1) = \frac{(n -1)!!}{n!!} \]

\(n!!\) is the double factorial of \(n\), i.e. \(1 \times 3 \times ... \times n\) if \(n\) is odd and \(2 \times 4 \times ... \times n\) if \(n\) is even.

Code

migdal <- function(n) {
  if (n == 1) {
    1
  } else {
    if (n %% 2 == 0) {
      prod(seq(1, n - 1, 2)) / prod(seq(2, n, 2))
    } else {
      prod(seq(2, n - 1, 2)) / prod(seq(1, n, 2))
    }
  }
}

sim_probs <- 1:20 |>
  map(\(n) mean(sim_games(n, 1)$traitors_win), .progress = TRUE) |>
  as.double()

migdal_probs <- 1:20 |>
  map(migdal) |>
  as.double()

ggplot(tibble(n_players = 1:20, sim_prob = sim_probs)) +
  aes(x = n_players, y = sim_prob) +
  geom_point(colour = "red") +
  geom_line(data = tibble(n_players = 1:20, migdal_prob = migdal_probs), mapping = aes(y = migdal_prob)) +
  scale_y_continuous(limits = c(0, 1.5))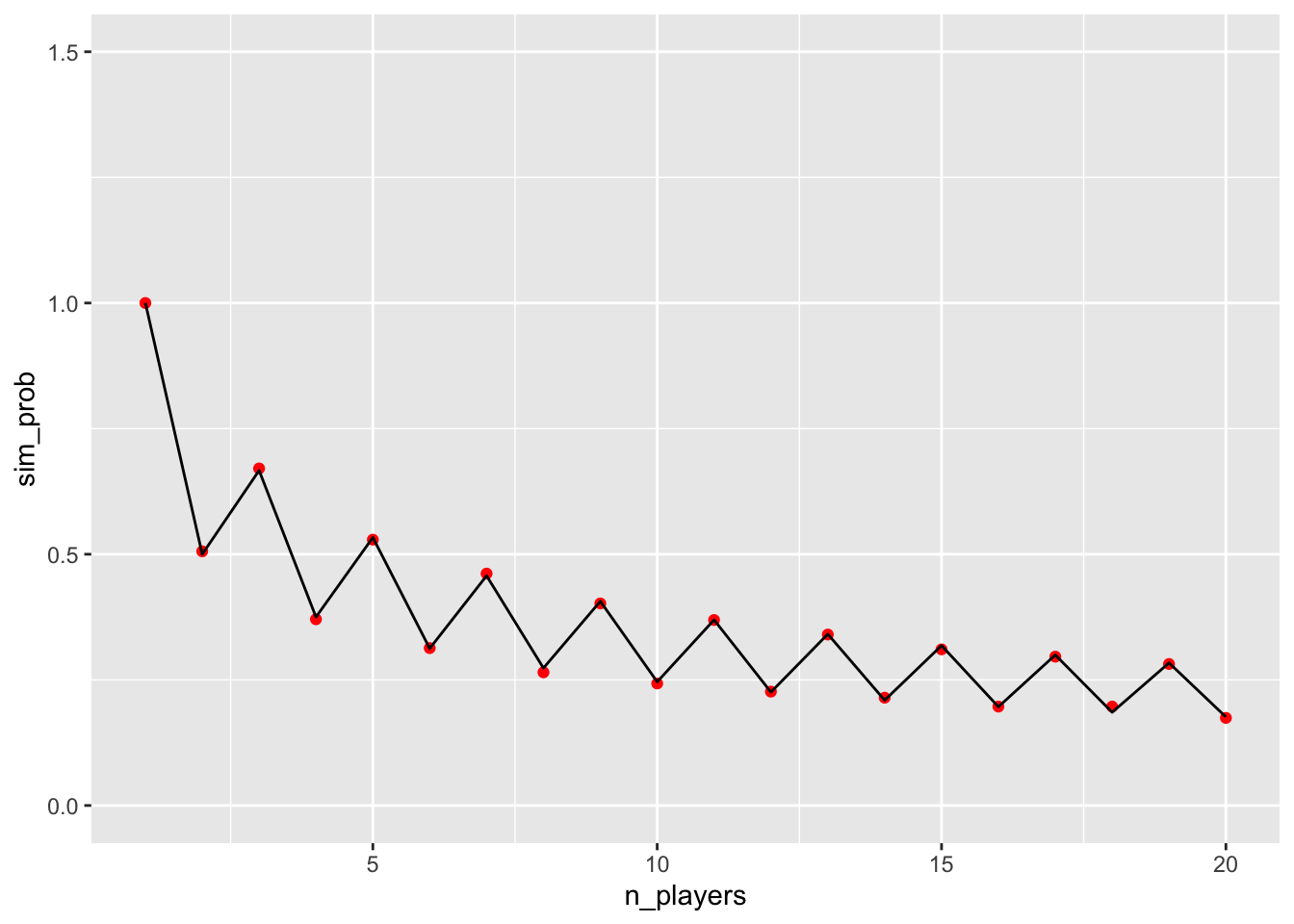

Figure 3: Comparison of simulated (points) to calculated (line) win probabilities.

The sawtooth pattern is one of the interesting results of Migdał’s paper: an odd number of players strongly favours the traitors, to the extent that having 8 faithful and 1 traitor gives the traitor a better win chance than having 3 faithful and 1 traitor, despite there being more than twice as many faithful in the former.

That has a useful implication for the producers of the Traitors: if they want to keep the game balanced, the timing of adding new players is crucial. I suspect they already know this.

How good is our random vote assumption?

Let’s see how random the votes actually are. Happily, Traitors is a big enough phenomenon that people have recorded the players’ votes online. Here for example are the votes from Australia’s first season. Below the fold is some code for manipulating the copy-pasted votes into a dataframe.

Code

# Some fixes were required: in Aus two players abstained from a vote, and one quit.
# I converted these into pseudo-votes for an imaginary player.

votes <- list(
  # Aus 1
  list(
    c(20, 2, 1),
    c(16, 2, 1, 1, 1),
    c(4, 4, 3, 3, 2, 1, 1, 1),
    c(11, 5, 2),
    c(7, 6, 2, 1),
    c(7, 5, 1, 1),
    c(9, 3, 1),
    c(9, 1, 1),
    c(8, 2),
    c(4, 1, 1, 1, 1),
    c(5, 1, 1),
    c(4, 1),
    c(3, 1),
    c(2, 1)
  ),

  # UK 1
  list(
    c(11, 8),
    c(8, 6, 3),
    c(11, 4),
    c(9, 4),
    c(7, 3, 1),
    c(7, 1, 1),
    c(6, 2),
    c(4, 2),
    c(3, 2),
    c(1, 3),
    c(3, 0)
  ),

  # UK 2
  list(
    c(17, 1, 1),
    c(10, 6, 1),
    c(7, 6, 2, 1),
    c(7, 4, 1, 1, 1),
    c(6, 5, 2, 1),
    c(7, 3, 2, 1),
    c(6, 2, 2),
    c(4, 2, 1, 1),
    c(4, 2),
    c(4, 1),
    c(2, 2),
    c(3, 1),
    c(3, 0)
  ),

  # US
  list(
    c(15, 2, 2, 1, 1),
    c(4, 4, 4, 3, 1, 1, 1, 1),
    c(7, 6, 3),
    c(14, 1, 1, 1, 1),
    c(12, 2, 1, 1),
    c(7, 3, 2, 1, 1),
    c(9, 2, 1),
    c(7, 4),
    c(6, 2, 1),
    c(6, 1, 1),
    c(4, 1, 1),
    c(4, 1),
    c(4, 0),
    c(3, 1),
    c(1, 2),
    c(2, 1)
  )
)

pad <- function(v, new_length, value) {
  v2 <- rep(value, new_length)
  v2[1:length(v)] <- v
  v2
}

votes_df <- tibble(v = flatten(votes)) |>
  rowwise() |>
  filter(sum(v) > 5) |> # ignore the finals, which are a little different
  mutate(
    n_players = sum(v),
    v = list(pad(v, n_players, 0)), # pad 0s for with each player that didn't receive a vote
  )

We can guess by looking that these aren’t drawn from a uniform distribution, and \(\chi^2\) agrees.

votes_df |>
  mutate(p.value = chisq.test(v, simulate.p.value = TRUE)["p.value"]) |>
  unnest(p.value) |>
  head(5) |>  # the whole table is not that interesting
  kable(digits = 5)

Table 1: Completely unnecessary \(\chi^2\) goodness-of-fit tests.

v	n_players	p.value
20, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0	23	0.0005
16, 2, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0	21	0.0005
4, 4, 3, 3, 2, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0	19	0.0085
11, 5, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0	18	0.0005
7, 6, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0	16	0.0005

It looks to me like the faithful do herd together to whomp one or two unlucky players. Sometimes this is pre-arranged, sometimes it’s just groupthink (“I’ve just got nothing to go on, so I put yourself…”).

Let’s implement a voting strategy that’s closer to this reality. We’ll take the mean of the vote distributions as the probability of voting for target one, two, three, etc, to form a multinomial distribution, so that our simulation reflects actual vote distributions.

n_rounds <- nrow(votes_df)
n_players <- max(votes_df$n_players)

mat <- matrix(0, nrow = n_rounds, ncol = n_players)

for (i in 1:n_rounds) {
  v <- votes_df$v[[i]]
  mat[i, 1:length(v)] <- v / sum(v)
}

vote_prob <- colSums(mat) / nrow(mat)

barplot(vote_prob)

Figure 4: Mean of normalised vote counts across each round.

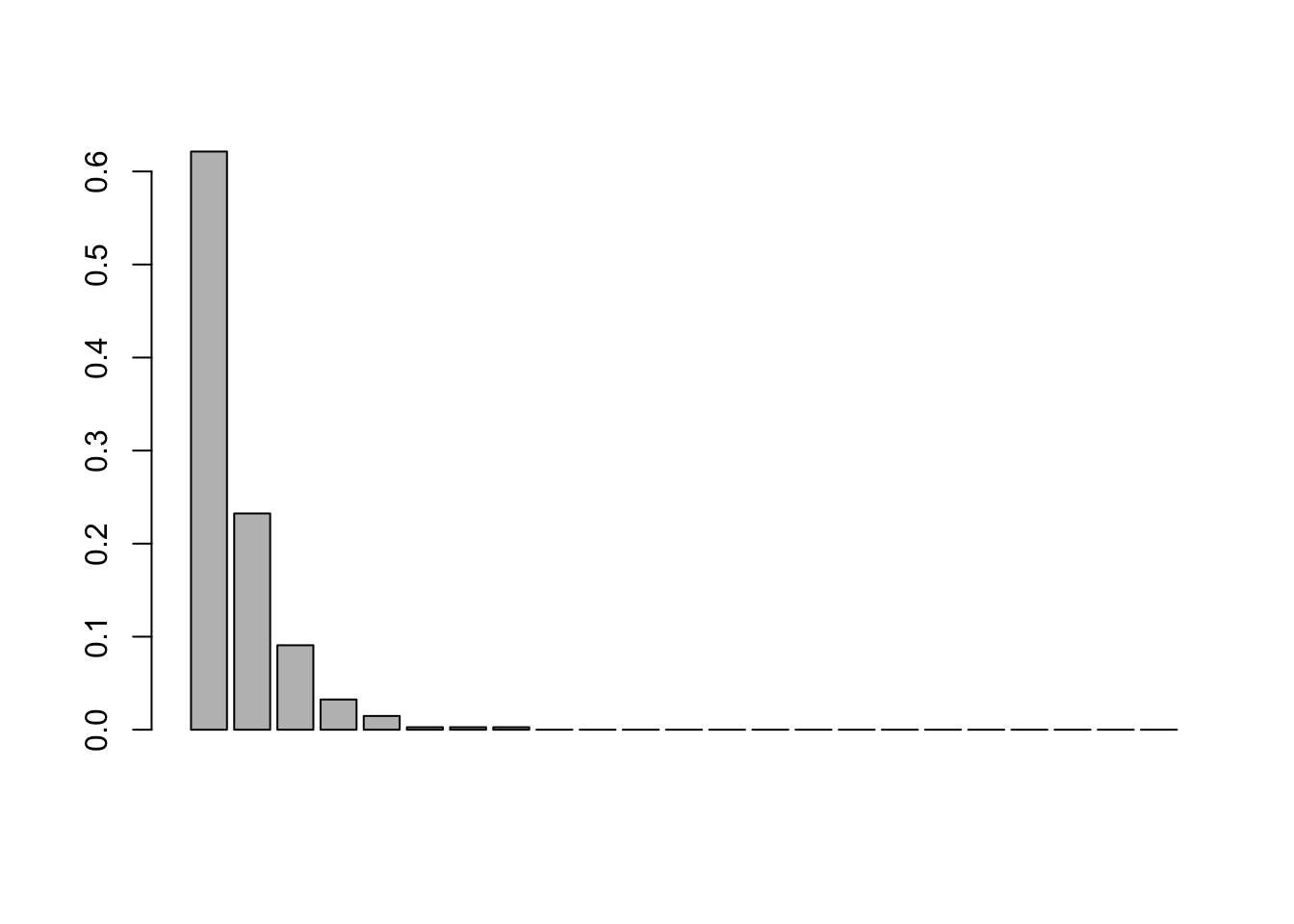
In a typical round, we’d expect about 62% of players to vote for player A, and 23% for player B, etc. This doesn’t relate to the probability of player A or B being traitors, just the expected vote split.

Let’s make that a strategy function and simulate it.

random_herd <- function(n_players, n_traitors) {
  shuffled <- sample(n_players, n_players)
  sample(shuffled, size = n_players - n_traitors, replace = TRUE, prob = vote_prob[1:n_players])
}

results <- sim_games(n_players = 22, n_traitors = 3, traitor_strategy = random_traitors, faithful_strategy = random_herd)
plot_game_results(results, 22, 3)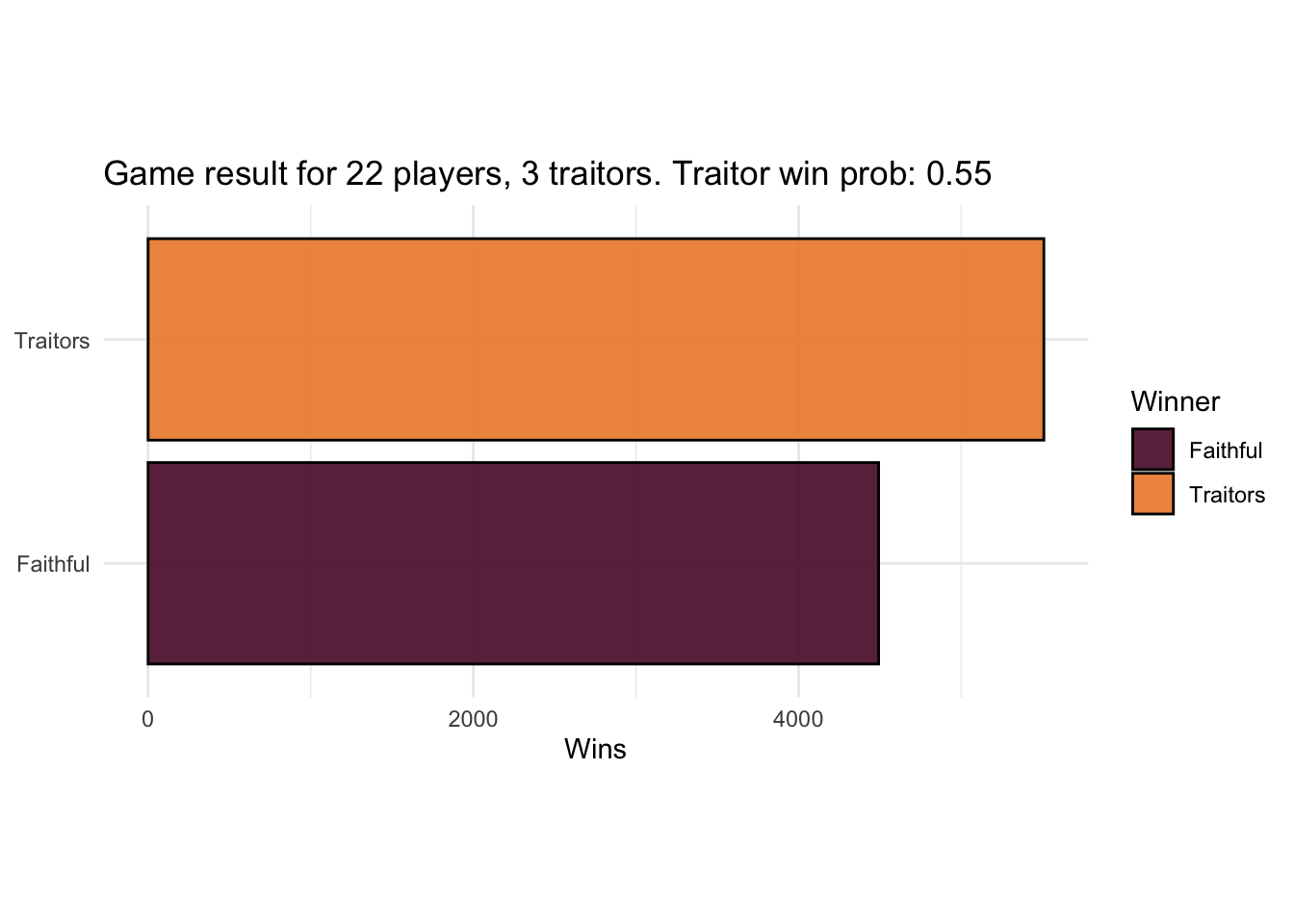

Having a split vote isn’t much worse than the fully random strategy, though it still gives the traitors a slight advantage. Could the faithfuls do better? Well yes, if they were any good at spotting traitors.

Smarter faithfuls

Let’s grant the faithfuls a glimmer of intuition: they are twice as suspicious of traitors as faithfuls, i.e. a traitor is twice as likely to be the vote target as a faithful. We’ll call that the suspicion factor, where a value of 1 means a traitor is equally suspicious as any other player to the faithfuls.

We can model this with a suspicion vector, which is the (normalised) level of suspicion for each player. We’ll need a new game function, which we’ll call game2. This version of the game allows both faithfuls and traitors to influence the suspicion on each player each day.

game2 <- function(
    n_players = 22,
    n_traitors = 3,
    traitors_influence = no_influence,
    faithfuls_influence = no_influence,
    traitors_strategy = random_traitors2,
    faithfuls_strategy = random_faithful2) {
  while (TRUE) {

    if (n_traitors == 0 || n_players - n_traitors < n_traitors) {
      break
    }

    #############
    # DAY PHASE #
    #############

    # This is the new bit:
    # traitors and faithfuls influence suspicion
    suspicions <- rep(1, n_players) |>
      faithfuls_influence(n_traitors) |>
      traitors_influence(n_traitors)
    suspicions <- suspicions / sum(suspicions)  # normalise

    # Voting is as-before
    votes <- rep(0, n_players)

    if (n_players - n_traitors == 1) {
      votes[1:n_traitors] <- n_players
    } else {
      votes[1:n_traitors] <- traitors_strategy(suspicions, n_players, n_traitors)
    }
    votes[(n_traitors + 1):n_players] <- faithfuls_strategy(suspicions, n_players, n_traitors)

    banished <- which.max(tabulate(votes))

    n_players <- n_players - 1 # BANISHMENT!
    if (banished <= n_traitors) {
      n_traitors <- n_traitors - 1
    }

    if (n_traitors == 0 || n_players - n_traitors < n_traitors) {
      break
    }

    ###############
    # NIGHT PHASE #
    ###############
    n_players <- n_players - 1 # MURDER!
  }

  list(n_players_remaining = n_players, n_traitors_remaining = n_traitors)
}

random_faithful2 <- function(suspicions, n_players, n_traitors) {
  # vote for a single random player
  target <- sample(1:n_players, size = 1)
  rep(target, n_players - n_traitors)
}

random_traitors2 <- function(suspicions, n_players, n_traitors) {
  # as before: vote a single random faithful
  target <- sample((n_traitors + 1):n_players, size = 1)
  rep(target, n_traitors)
}

no_influence <- function(suspicions, n_traitors) suspicions

We set the default influence to be a pass-through i.e. no influence, and set the same default vote strategies as before (adapted to accept but ignore a suspicions argument). In that case we see that the game is balanced the same as before. That’s a useful sanity check.

results <- sim_games(.game = game2)
plot_game_results(results, 22, 3)

We can check with the random herd strategy too.

random_herd2 <- function(suspicion, n_players, n_traitors) {
  shuffled <- sample(n_players, n_players)
  sample(shuffled, size = n_players - n_traitors, replace = TRUE, prob = vote_prob[1:n_players])
}

results <- sim_games(faithfuls_strategy = random_herd2, .game = game2)
plot_game_results(results, 22, 3)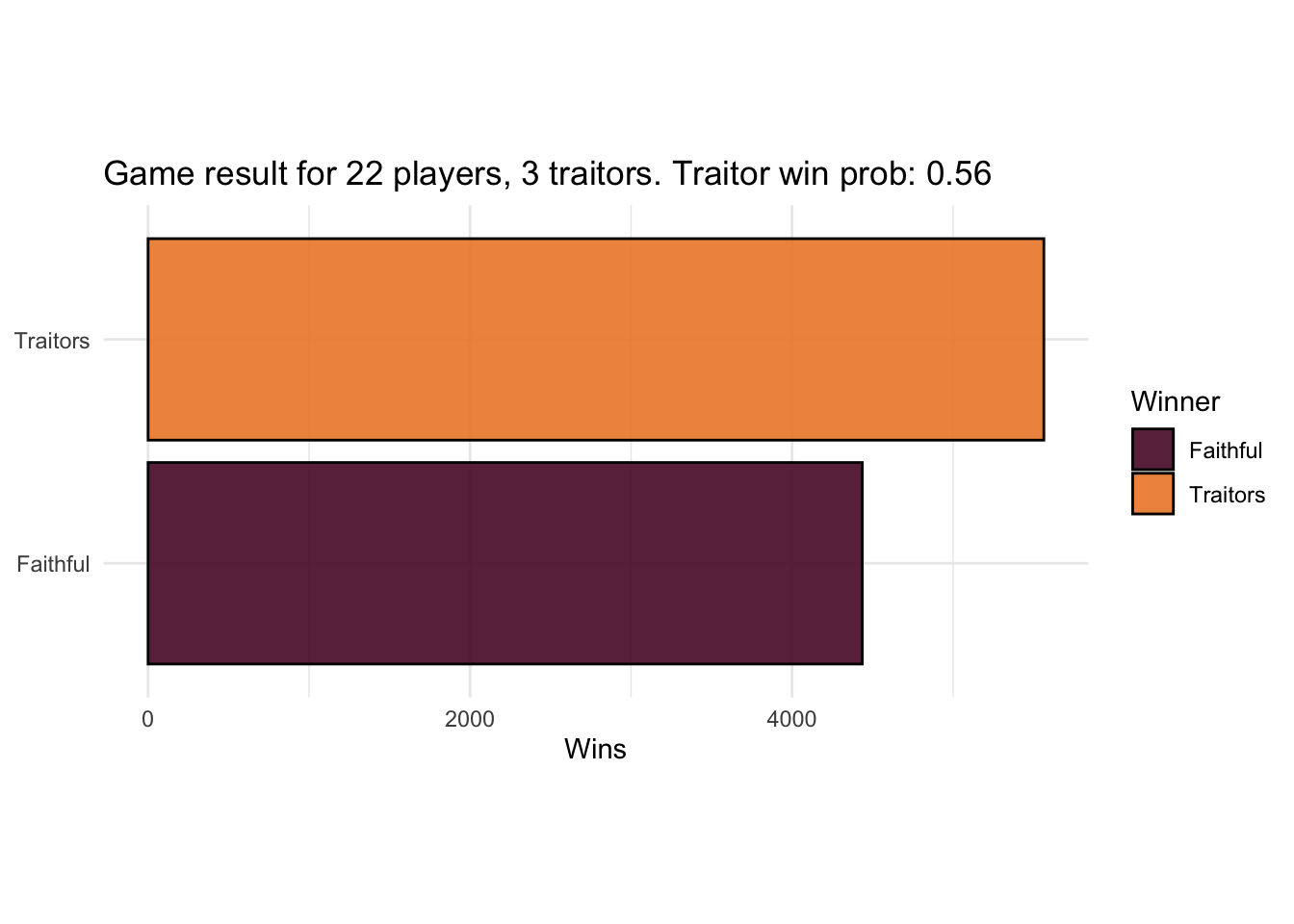

Also the same. But now let’s grant the faithfuls some strong intuition, twice as much suspicion on traitors as faithfuls. To support different levels of suspicion we can use a closure.

increased_suspicion <- function(suspicion_factor) {
  function(suspicions, n_traitors) {
    suspicions[1:n_traitors] <- suspicion_factor
    suspicions
  }
}

# e.g. increased_suspicion(2) returns a function that updates the traitors' suspicion values to 2

We also define a version of the herd strategy that selects the players to whomp according to their relative suspicion.

suspicious_herd <- function(suspicions, n_players, n_traitors) {
  shuffled <- sample(n_players, size = n_players, prob = suspicions)
  sample(shuffled, size = n_players - n_traitors, replace = TRUE, prob = vote_prob[1:n_players])
}

How does that shake out for the faithfuls?

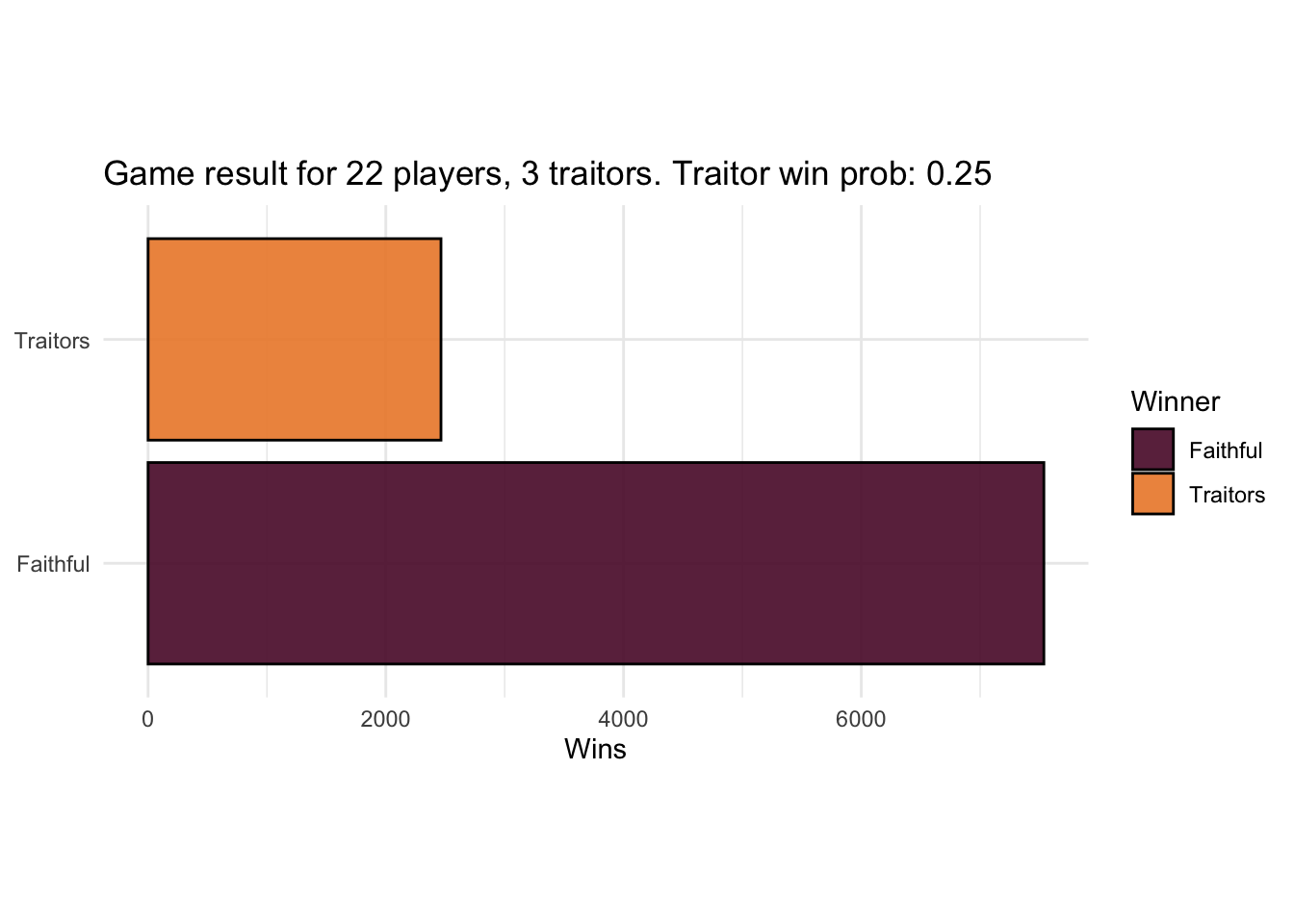
results <- sim_games(faithfuls_influence = increased_suspicion(2), faithfuls_strategy = suspicious_herd, .game = game2)
plot_game_results(results, 22, 3)

Magnificently! That puts the balance resoundingly in favour of the faithfuls, showing how fragile the traitors’ position really is. We can explore how the traitors’ win probability depends on how savvy the faithful are.

suspicions <- c(0.5, 1.0, 1.2, 1.5, 2.0, 5.0, 10.0)
s_df <- suspicions |>
  map(
    \(s)
    sim_games(
      n_players = 22,
      n_traitors = 3,
      faithfuls_influence = increased_suspicion(s),
      faithfuls_strategy = suspicious_herd,
      .game = game2
    ) |>
      mutate(suspicion = s),
    .progress = TRUE
  ) |>
  bind_rows() |>
  group_by(suspicion) |>
  summarise(traitor_win_prob = mean(traitors_win))

 ■■■■■■■■■■■■■■■■■■■■■■■■■■■       86% |  ETA:  2s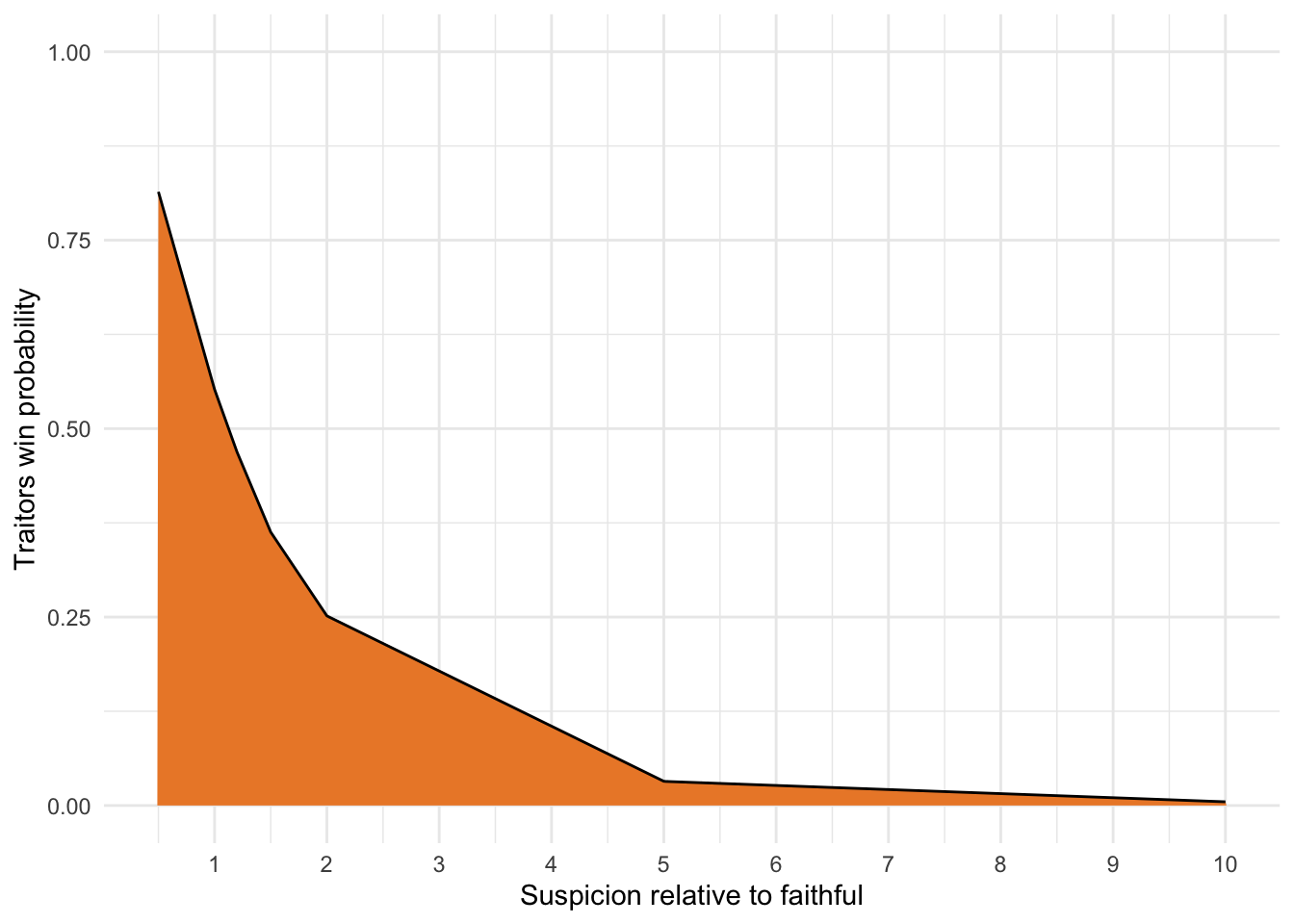

ggplot(s_df) +
  aes(x = suspicion, y = traitor_win_prob) +
  geom_area(fill = orange, colour = "black") +
  scale_x_continuous(breaks = seq(0, 10, 1)) +
  scale_y_continuous(limits = c(0, 1)) +
  labs(
    x = "Suspicion relative to faithful",
    y = "Traitors win probability"
  ) +
  theme_minimal()

Figure 9: Traitor win probability as a function of suspicion.

The odds get exponentially worse the more the faithful suspect the traitors. And vice-versa: if the traitors are less-suspected than the faithful, they stand a strong chance of winning the game.

Smarter traitors

Naturally the traitors will try to influence faithfuls towards other faithfuls. (Or other traitors, but let’s leave that strategy aside for now.) We could model that as the traitors being able to increase the suspicion level of other players. If they have limited influence, perhaps it makes sense for them to make a concerted effort to put suspicion on one other player.

sow_suspicion <- function(suspicion_factor) {
  function(suspicions, n_traitors) {
    suspicions[n_traitors + 1] <- suspicion_factor
    suspicions
  }
}

results <- sim_games(
  traitors_influence = sow_suspicion(2),
  faithfuls_influence = increased_suspicion(2),
  faithfuls_strategy = suspicious_herd,
  .game = game2
)
plot_game_results(results, 22, 3)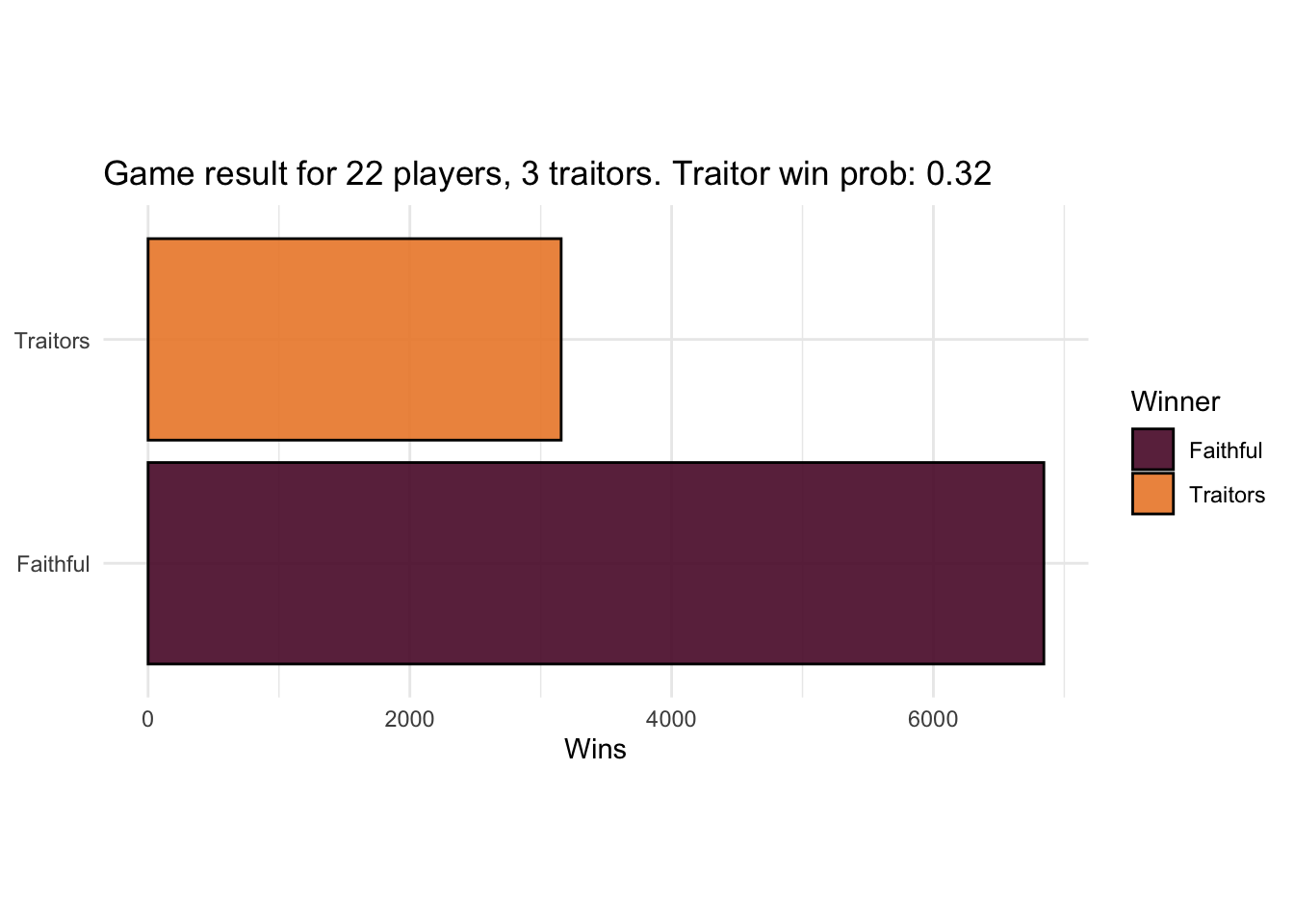

It’s an improvement! They’ve dragged the win probability from 0.24 up to 0.32. To completely nullify the faithfuls’ advantage though they would need to sow enough suspicion to make the traitors below the group’s mean level of suspicion.

Happily for the traitors, the faithfuls seem likely to manage that themselves, by fixating on a “twinkle in the eye” or other red herrings. As we’ve seen, it’s enough for the traitors to wait for faithfuls to get suspicious of another faithful and run with that.

Where next?

All models are wrong, especially yours Chris.

George Box (ghost of)

It hardly needs to be said that this model is a much-simplified version of reality. We’ve barely touched on the psychological aspects that make the game so fun, as well as many of the TV’s specific game mechanics:

shields
recruitment
the final

Those would certainly change the balance.

At the moment the suspicions vector is also too simplistic. I was tempted to make some kind of model that draws suspicions from a Dirichlet distribution, but decided that making a more complex model to simulate player behaviour that is sometimes almost chaotic is probably not a productive route.

There’s more we could do with the model we have so far too, for example looking at how the traitor win probability increases as the game progresses. For example at the time of writing, the Season 3 in the UK has 8 faithfuls and 2 traitors, with one murder pending. If we repeat the last result with those numbers, the traitors are on-track to win.

results <- sim_games(
  n_players = 7,
  n_traitors = 2,
  traitors_influence = sow_suspicion(2),
  faithfuls_influence = increased_suspicion(2),
  faithfuls_strategy = suspicious_herd,
  .game = game2
)
plot_game_results(results, 7, 2)

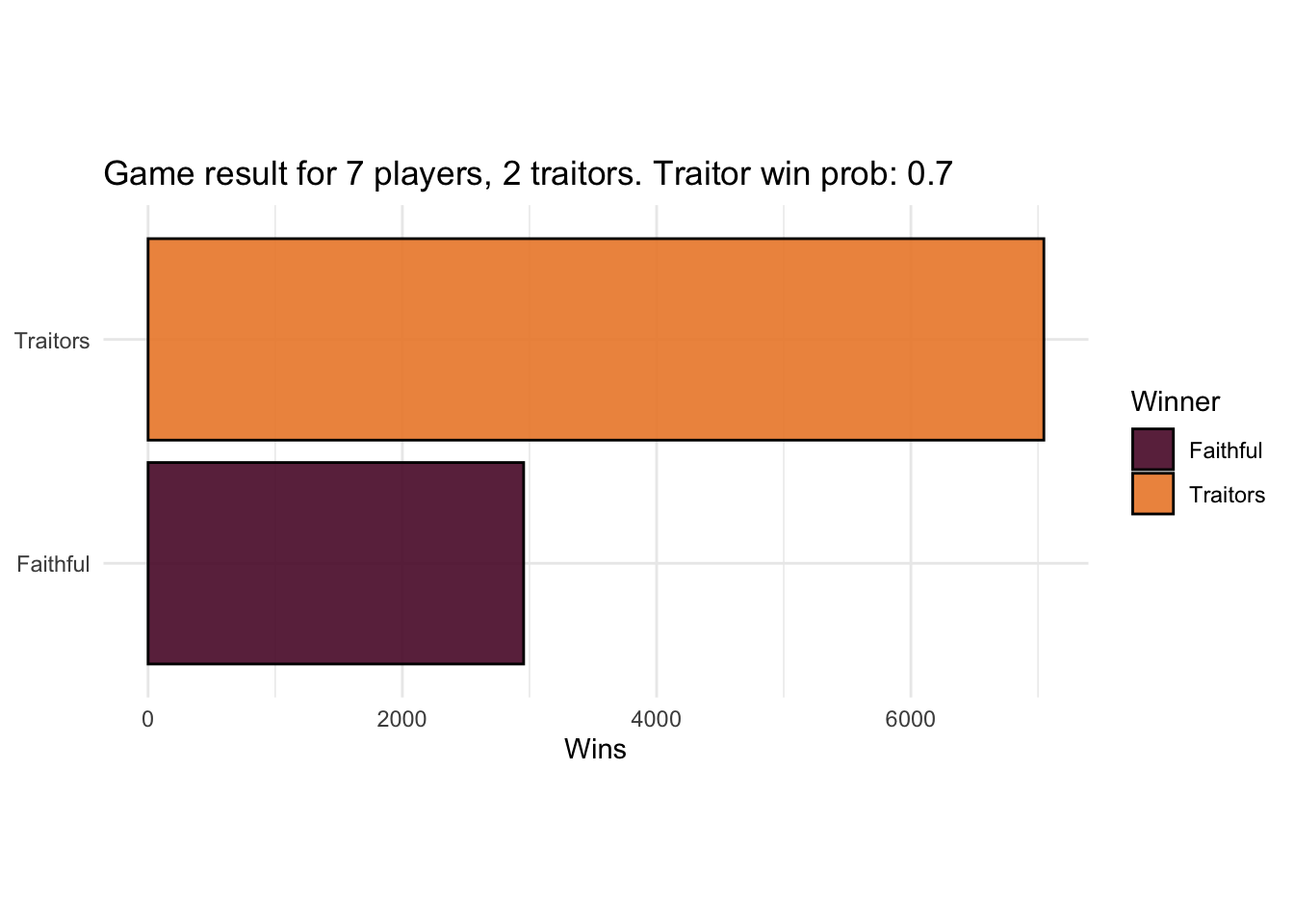
Incidentally, the traitors decided against recruitment. However that would have been an even better move.

results <- sim_games(
  n_players = 8,
  n_traitors = 3,
  traitors_influence = sow_suspicion(2),
  faithfuls_influence = increased_suspicion(2),
  faithfuls_strategy = suspicious_herd,
  .game = game2
)
plot_game_results(results, 8, 3)

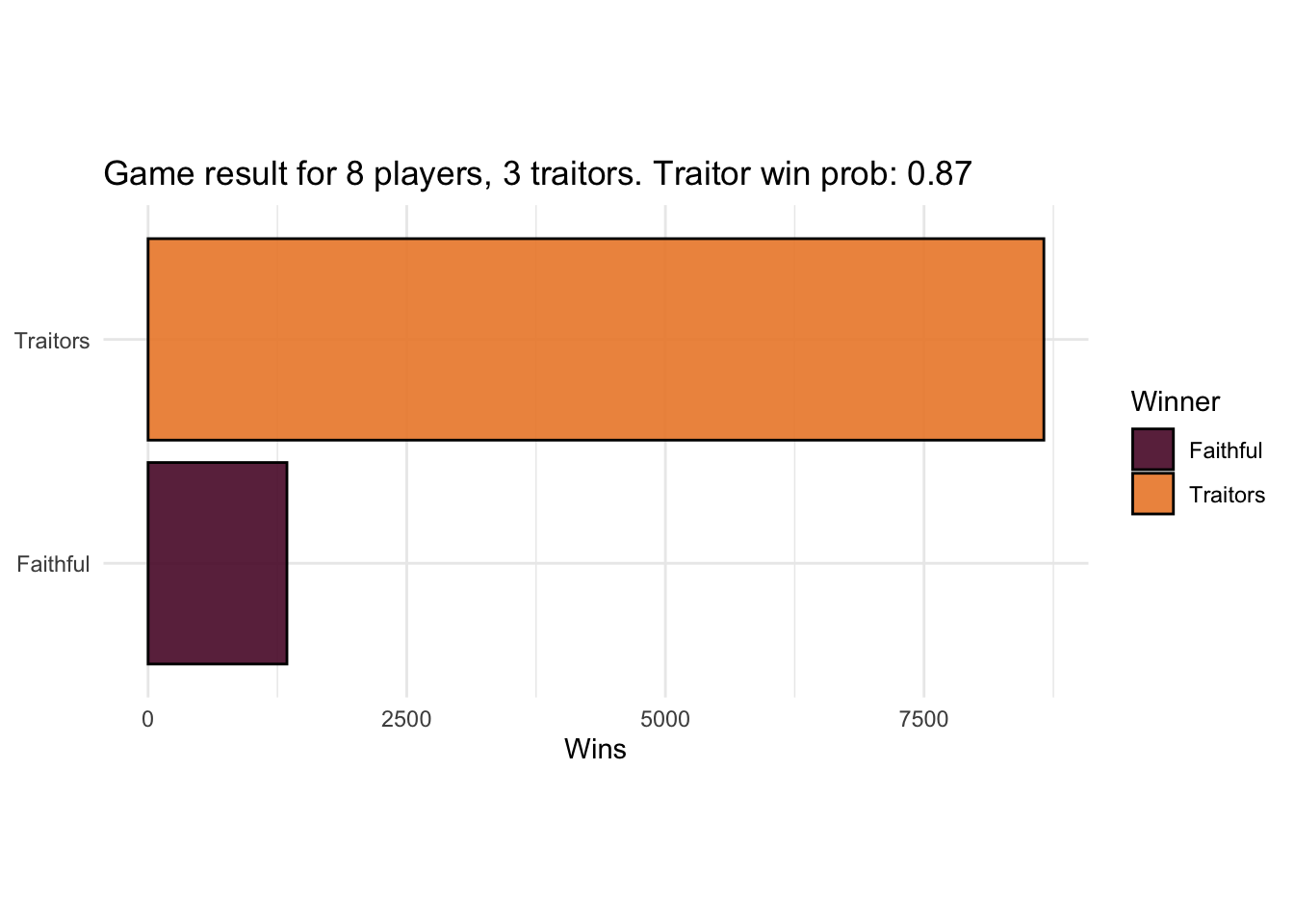
Somebody better teach those traitors to screw around with code!