Importance Sampling – Chris Bowdon

The aim of this post is to teach myself basic Bayesian methods. I’ll set up a toy example problem and solve it.

Let’s assume we have a natural event that happens with a variable periodicity e.g. a woman’s menstrual cycle. I’m drawing from this excellent blog on predicting a pregnancy, but doing a much simpler model because I am but a baby myself.

The aim here is to see if we can find the mean period of the cycle given some samples and priors for the average cycle. First, priors from the blog linked above:

# a normal distribution for the mean days between period starts
prior_mean_mu <- 27.7
prior_mean_sd <- 2.4
# a half-normal distribution for the SD of days between period starts
prior_sd_mu <- 1.6
prior_sd_sd <- 2.05

We will set the true mean and SD (the params, \(\theta\), that we’re looking for) and simulate some sample data, \(d\).

Code

library(tidyverse)
set.seed(42)

true_mu <- 26.3
true_sd <- 1.9

sample_periods <- rnorm(12, true_mu, true_sd)

For importance sampling we need a likelihood function, \(L(d|\theta)\). Make the model a normal distribution and this is simply the probability density. We take the log of the likelihood because the numbers could be very small and subject to numerical error.

log_likelihood <- function(sample_periods, mean_period, sd_period) {
  sum(dnorm(sample_periods, mean_period, sd_period, log = TRUE))
}

A little sanity check: the likelihood of the true parameters should be greater than the likelihood of the priors, for a large enough dataset.

ten_year_sample <- rnorm(120, true_mu, true_sd)
log_likelihood(ten_year_sample, true_mu, true_sd) > log_likelihood(ten_year_sample, prior_mean_mu, prior_mean_sd)

[1] TRUE

Importance sampling to fit the model

Importance sampling is a Monte Carlo method that is very easy to setup and that can work well if (1) the parameters space is small and (2) the priors are not too dissimilar from the posterior.

I know that both these conditions are true in my toy example.

First we must sample from the prior.

n_samples <- 100000
prior <- tibble(
  mu_period = rnorm(n_samples, prior_mean_mu, prior_mean_sd),
  sd_period = abs(rnorm(n_samples, 0, prior_sd_sd))
)

ggplot(prior) +
  aes(x = mu_period) +
  geom_histogram(alpha=0.5, colour="black", linewidth=0.1, fill="dodgerblue4")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

ggplot(prior) +
  aes(x = sd_period) +
  geom_histogram(alpha=0.5, colour="black", linewidth=0.1, fill="dodgerblue4")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Then we weight each draw by its likelihood.

weights <- sapply(1:n_samples, function(i) {
  log_likelihood(sample_periods, prior$mu_period[i], prior$sd_period[i])
})

Then we resample the prior by this weighting.

# n.b. sample will normalise the weights
posterior <- prior[sample(n_samples, replace = TRUE, prob = exp(weights)), ]

df <- bind_rows(
  mutate(prior, dist = "prior"),
  mutate(posterior, dist = "posterior")
) |>
  pivot_longer(c(mu_period, sd_period), names_to = "param", values_to = "value")

ggplot(df) +
  aes(x = value, fill = dist) +
  facet_wrap(vars(param), scales = "free") +
  scale_fill_manual(values=c("dodgerblue1", "dodgerblue4")) +
  geom_histogram(alpha = 0.5, colour="black", linewidth=0.1, position = "identity")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.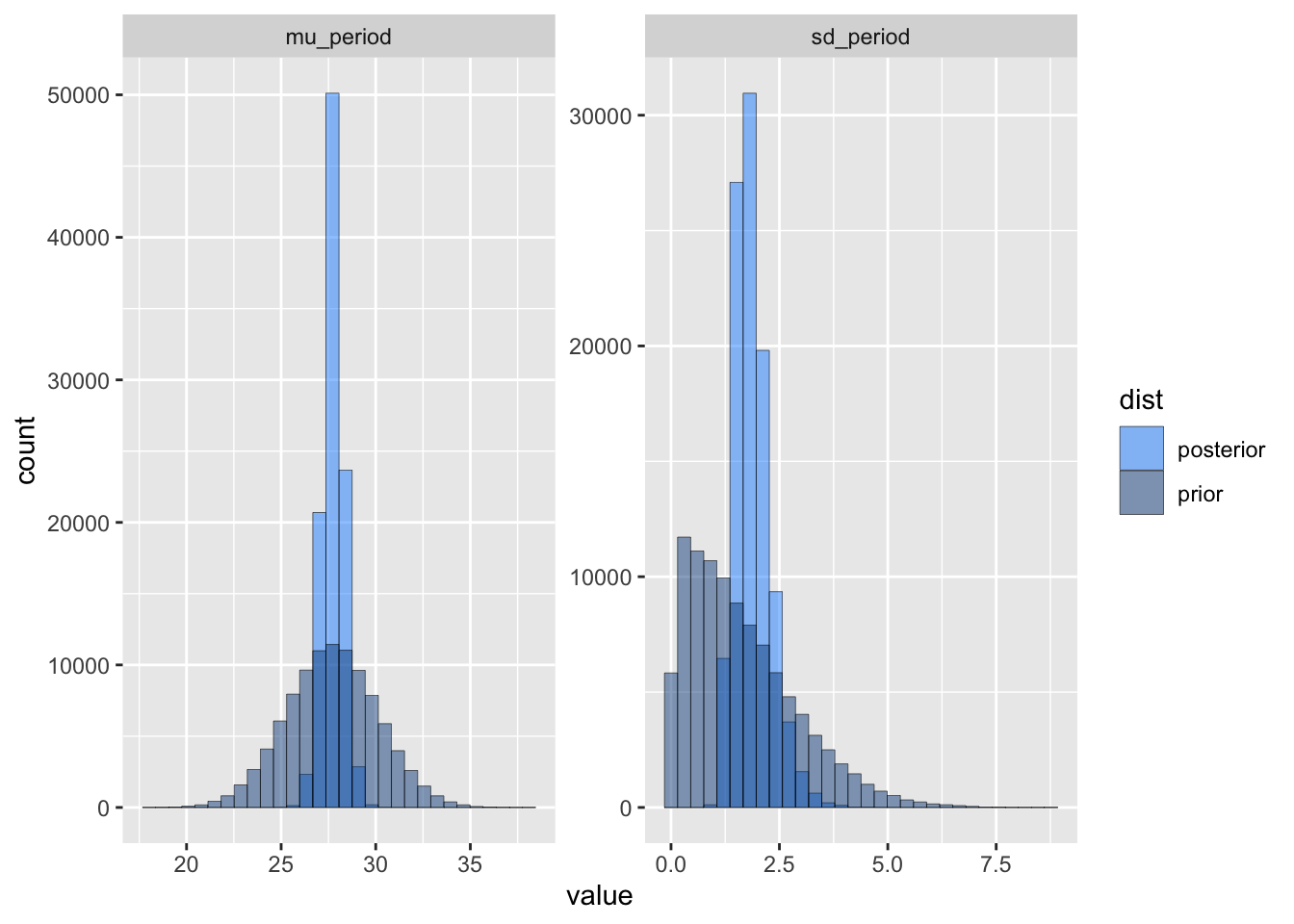

Hey Doctor, would you look at that! The posterior is much tighter and closer to the true values.

posterior |> summarise(mu = mean(mu_period), sd = mean(sd_period))

# A tibble: 1 × 2
     mu    sd
  <dbl> <dbl>
1  27.7  1.88

How does that compare to simply taking the mean and SD of the sample data?

tibble(
    mu = mean(sample_periods),
    sd = sd(sample_periods)
)

# A tibble: 1 × 2
     mu    sd
  <dbl> <dbl>
1  27.7  1.75

It’s not highly convincing in this case. I ran this a few times and it seemed that the SD estimation seemed to be closer to the true value than the SD of the sample, but the mean was rarely different. This is probably because it’s a very simple model and importance sampling is rather overkill.

Proposal distribution isn’t necessarily the prior

In Bååth’s other blog on importance sampling he explains that we are looking at the ratio of the likelihood of getting our sample from the target distribution relative to getting it from the proposal distribution (then normalised to form a new estimate of the target distribution).

If the proposal distribution is thinner at the ends than the target distribution, this is suboptimal because we will have fewer samples there. So a T distribution is a useful proposal for a normal target, because it has fatter tails (as controlled by the df degrees of freedom parameter).

We could choose a very sloppy proposal like a uniform distribution, but in that case we are suboptimal in terms of how quickly we explore the space. We would have a relatively high number of samples in the tails compared to the peak. Bååth has a neat method of using a Laplacian approximation as a proposal.

Quick look at another example

Now an example from this blog post. This one uses a T as the proposal.

approx_samples <- rt(100, df = 3)  # T with 3 deg free is our approximation to posterior
approx_density <- dt(approx_samples, df = 3, log = TRUE)  # get the prob density for each
unnormalised_posterior <- dnorm(approx_samples, log = TRUE, sd = sqrt(3))  # convert to actual posterior

# weights are then...
log_imp_weights <- unnormalised_posterior - approx_density
data.frame(log_imp_weights) %>% 
  ggplot(aes(exp(log_imp_weights))) +
  geom_density(fill = "dodgerblue4", alpha = 0.5) +
  labs(title = "Importance weights",
       subtitle = "Approximating a normal with a t distribution")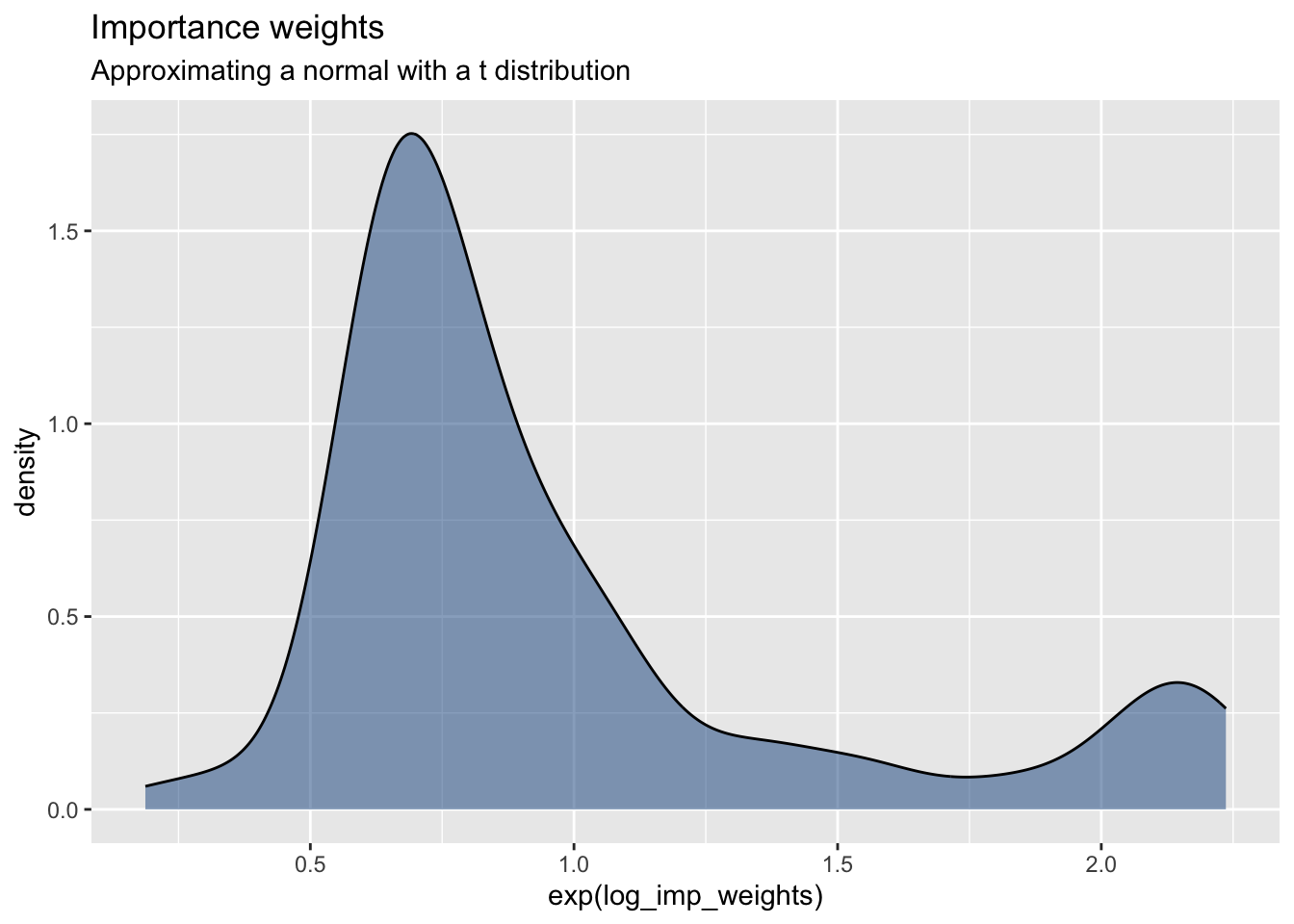

# normalise...
weights <- exp(log_imp_weights) / sum(exp(log_imp_weights))

mean_estimate <- sum(approx_samples * weights)

The point of using the Student T distribution as the proposal is to have a proposal with better coverage of the tails.